زندگینامه توماس بیز؛ بنیانگذار قضیه بیز و پیشگام آمار مدرن

معرفی توماس بیز: دانشمند برجسته قرن هجدهم

توماس بیز (Thomas Bayes) یکی از برجسته‌ترین ریاضیدانان و آماردانان تاریخ است که نام او با یکی از مهم‌ترین قضایای نظریه احتمالات گره خورده است. او در سال ۱۷۰۱ میلادی در شهر لندن، پایتخت انگلستان، متولد شد و زندگی خود را وقف مطالعه و تحقیق در زمینه‌های مختلف علمی کرد. دستاوردهای علمی بیز تأثیر عمیقی بر توسعه علوم آماری، یادگیری ماشین، هوش مصنوعی و تصمیم‌گیری علمی داشته است.

دوران تحصیلات و آغاز مسیر علمی

توماس بیز پس از گذراندن دوران کودکی و تحصیلات ابتدایی در لندن، در سال ۱۷۱۹ میلادی وارد دانشگاه معتبر ادینبرگ در اسکاتلند شد. او در این دانشگاه در دو رشته منطق و الهیات به تحصیل پرداخت که هر دو رشته در آن زمان از اهمیت بالایی برخوردار بودند. دوران تحصیل در ادینبرگ نقطه عطفی در زندگی بیز محسوب می‌شود، چراکه در همین دوره بود که او با مفاهیم پیچیده ریاضیات و منطق آشنا شد.

از همان سال‌های جوانی، بیز علاقه وافری به علم ریاضیات و به‌ویژه شاخه‌ای که امروزه آن را نظریه احتمالات می‌نامیم، نشان داد. این علاقه فزاینده باعث شد تا او ساعت‌های طولانی را صرف مطالعه آثار ریاضیدانان پیشین و انجام تحقیقات شخصی در این زمینه کند. توماس بیز تلاش می‌کرد تا رابطه بین منطق، الهیات و ریاضیات را درک کند و این رویکرد میان‌رشته‌ای به او دیدگاه منحصربه‌فردی در حل مسائل علمی بخشید.

عضویت در انجمن سلطنتی و شناخت علمی

در سال ۱۷۴۲ میلادی، توماس بیز به عنوان یکی از اعضای برجسته انجمن سلطنتی انگلستان (Royal Society) انتخاب شد. این انتخاب نشان‌دهنده اعتبار و جایگاه علمی بالای او در جامعه علمی آن دوران بود. انجمن سلطنتی یکی از معتبرترین نهادهای علمی جهان محسوب می‌شد و عضویت در آن افتخار بزرگی برای هر دانشمند به شمار می‌رفت.

بیز تا پایان عمر خود این مقام را حفظ کرد و در طول این سال‌ها با بسیاری از دانشمندان برجسته زمان خود در ارتباط بود. او نه‌تنها به‌عنوان یک ریاضیدان، بلکه به‌عنوان یک متفکر و محقق چندبعدی شناخته می‌شد که می‌توانست پل ارتباطی بین علوم مختلف باشد.

تمرکز بر آمار و احتمالات: دهه ۱۷۴۰

از اوایل دهه ۱۷۴۰ میلادی به بعد، توماس بیز تقریباً تمام وقت و انرژی خود را بر مطالعه و تحقیق در زمینه آمار و نظریه احتمالات متمرکز کرد. او به این نتیجه رسیده بود که بسیاری از پدیده‌های طبیعی و اجتماعی را نمی‌توان با قطعیت کامل پیش‌بینی کرد و برای درک بهتر جهان، نیاز به ابزارهای ریاضی پیچیده‌تری داریم.

در این دوره، بیز سعی داشت تا روش‌هایی برای محاسبه احتمالات پیچیده ارائه دهد، به‌ویژه در شرایطی که اطلاعات کامل در دسترس نیست. این رویکرد کاملاً نوآورانه بود و پایه‌های تفکر استنتاج آماری مدرن را بنا نهاد. او باور داشت که می‌توان با استفاده از اطلاعات موجود و به‌روزرسانی باورها، به تصمیمات بهتری دست یافت.

قضیه بیز: میراث ماندگار یک دانشمند

تولد و انتشار قضیه بیز

مهمترین و شناخته‌شده‌ترین دستاورد علمی توماس بیز، قضیه معروف بیز (Bayes' Theorem) در نظریه احتمالات است. این قضیه یکی از بنیادی‌ترین اصول در آمار استنتاجی به شمار می‌رود و کاربردهای گسترده‌ای در علوم مختلف دارد. با این حال، توماس بیز هرگز نتوانست این اثر مهم را در طول زندگی خود منتشر کند.

در سال ۱۷۵۵، بیز دچار بیماری شد و پس از مدتی رنج، در سال ۱۷۶۱ میلادی دار فانی را وداع گفت. او بدون اینکه شاهد تأثیر عظیم کارهای خود بر جامعه علمی باشد، درگذشت. خوشبختانه، ریچارد پرایس (Richard Price)، دوست و همکار علمی بیز، پس از مرگ او اسناد و یادداشت‌های علمی وی را مرتب کرد و در سال ۱۷۶۳ آنها را منتشر ساخت.

چیستی و اهمیت قضیه بیز

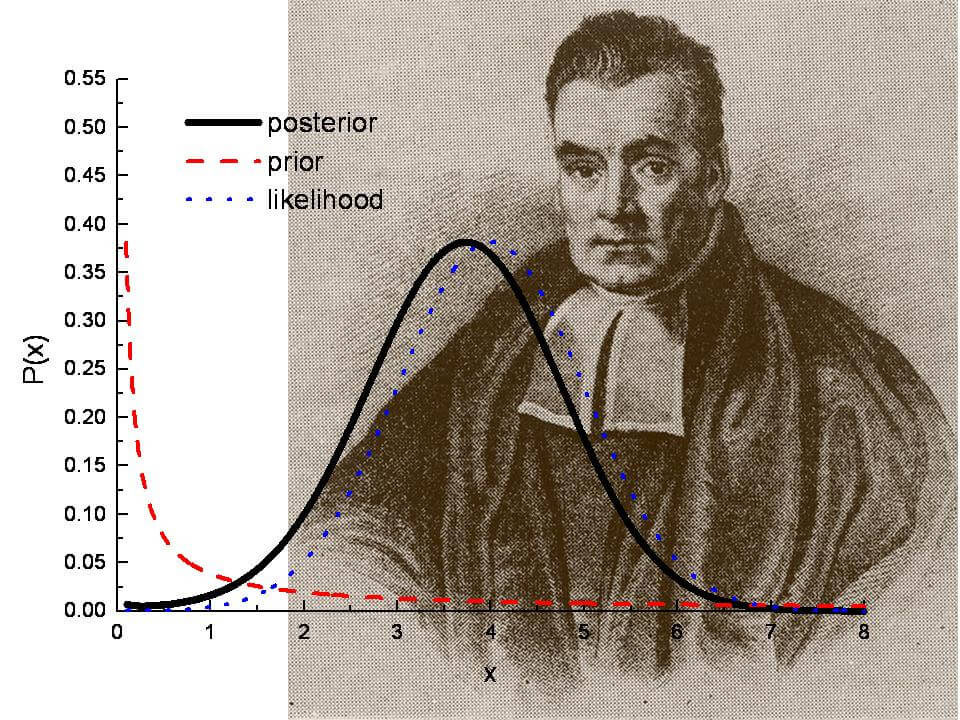
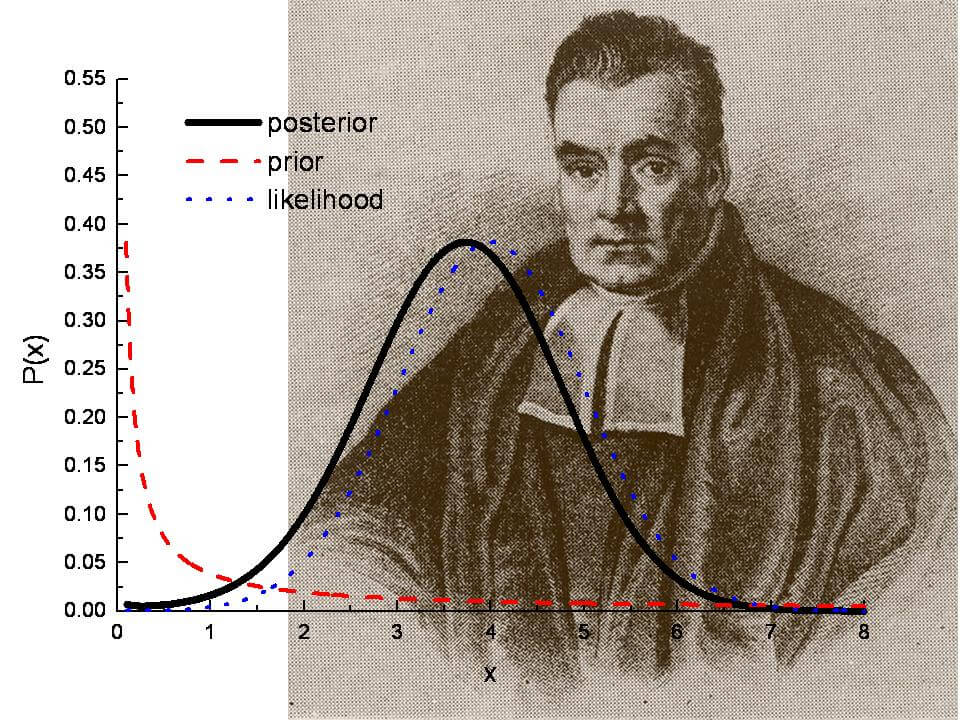
قضیه بیز روشی ریاضی برای به‌روزرسانی باورها و احتمالات بر اساس شواهد جدید است. این قضیه به ما می‌آموزد که چگونه می‌توانیم احتمال وقوع یک رویداد را با در نظر گرفتن اطلاعات جدید محاسبه کنیم. به بیان ساده‌تر، قضیه بیز ابزاری است برای دسته‌بندی پدیده‌ها بر پایه احتمال وقوع یا عدم وقوع آنها.

این قضیه از آن جهت بسیار مفید و کاربردی است که می‌توان از طریق آن احتمال یک پیشامد را با مشروط کردن نسبت به وقوع یا عدم وقوع یک پیشامد دیگر محاسبه کرد. در بسیاری از موقعیت‌های واقعی، محاسبه مستقیم احتمال یک رویداد بسیار دشوار یا حتی غیرممکن است. با استفاده از قضیه بیز و مشروط کردن پیشامد مورد نظر نسبت به پیشامدهای دیگر که اطلاعات بیشتری در مورد آنها داریم، می‌توان به احتمال دقیق‌تری دست یافت.

کاربردهای عملی قضیه بیز

امروزه قضیه بیز در حوزه‌های متنوعی کاربرد دارد:

• پزشکی و تشخیص بیماری: محاسبه احتمال ابتلا به یک بیماری با توجه به نتایج آزمایش‌ها
• یادگیری ماشین و هوش مصنوعی: الگوریتم‌های طبقه‌بندی و پیش‌بینی
• فیلترینگ هرزنامه: تشخیص ایمیل‌های اسپم از ایمیل‌های معتبر
• تحلیل ریسک مالی: ارزیابی خطرات سرمایه‌گذاری
• علوم اجتماعی: پیش‌بینی رفتارهای انسانی و تحلیل نظرسنجی‌ها
• حقوق و قضاوت: ارزیابی شواهد در دادگاه‌ها

تأثیر قضیه بیز بر توسعه علم احتمالات

قضیه بیز کمک بسیار زیادی به توسعه علم احتمالات و آمار مدرن کرد. این قضیه تحولی بزرگ در دوران خود برای درک بهتر پدیده‌های احتمالی به وجود آورد و راه را برای رویکردهای جدید در تفکر علمی باز کرد. پیش از آن، بسیاری از دانشمندان معتقد بودند که احتمالات باید بر اساس فرکانس‌های بلندمدت محاسبه شوند، اما قضیه بیز نشان داد که می‌توان احتمالات را به‌عنوان میزان اطمینان یا باور نسبت به یک گزاره در نظر گرفت.

امروزه، استنتاج بیزی (Bayesian Inference) یکی از دو رویکرد اصلی در آمار است که در کنار رویکرد فرکانسی جایگاه ویژه‌ای دارد. بسیاری از پیشرفت‌های اخیر در یادگیری ماشین، به‌ویژه در زمینه شبکه‌های عصبی و مدل‌های احتمالاتی، بر پایه اصول بیزی بنا شده‌اند.

میراث علمی و تأثیرگذاری ماندگار

هرچند توماس بیز بیش از دو قرن پیش درگذشت، اما نام او در تاریخ علم ثبت شده و میراث علمی‌اش همچنان زنده است. او نشان داد که چگونه می‌توان با استفاده از منطق ریاضی، عدم قطعیت را مدل‌سازی کرد و تصمیمات بهتری در شرایط نامشخص گرفت.

امروزه در عصر داده‌های کلان و هوش مصنوعی، اهمیت کار توماس بیز بیش از پیش آشکار شده است. بسیاری از الگوریتم‌هایی که در گوشی‌های هوشمند، موتورهای جستجو، سیستم‌های توصیه‌گر و حتی خودروهای خودران استفاده می‌شوند، بر پایه اصول بیزی طراحی شده‌اند.

نتیجه‌گیری

توماس بیز، ریاضیدان و محقق انگلیسی قرن هجدهم، با ارائه قضیه مشهور خود، پایه‌های یکی از مهمترین شاخه‌های آمار مدرن را بنا نهاد. زندگی او نمونه‌ای از تعهد به دانش و پیگیری کنجکاوی علمی است. قضیه بیز نه‌تنها در زمان خود تحولی بزرگ ایجاد کرد، بلکه امروزه نیز به‌عنوان یکی از ابزارهای اساسی در علوم داده، یادگیری ماشین و تصمیم‌گیری تحت عدم قطعیت کاربرد گسترده دارد. میراث توماس بیز یادآور این نکته است که ایده‌های بزرگ علمی ممکن است در زمان خود به‌طور کامل درک نشوند، اما ارزش واقعی آنها با گذشت زمان آشکار می‌شود.

منبع : WIKIPEDIA